Example: DC-DC converter solved by Uniform grid abstraction.
We consider a boost DC-DC converter which has been widely studied from the point of view of hybrid control, see for example in [1, V.A],[2],[3]. This is a safety problem for a switching system.
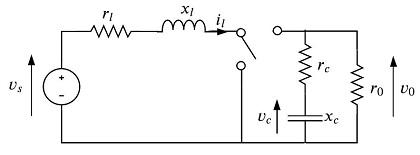
The state of the system is given by $x(t) = \begin{bmatrix} i_l(t) & v_c(t) \end{bmatrix}^\top$. The switching system has two modes consisting in two-dimensional affine dynamics:
\[\dot{x} = f_p(x) = A_p x + b_p,\quad p=1,2\]
with
\[A_1 = \begin{bmatrix} -\frac{r_l}{x_l} &0 \\ 0 & -\frac{1}{x_c}\frac{1}{r_0+r_c} \end{bmatrix}, A_2= \begin{bmatrix} -\frac{1}{x_l}\left(r_l+\frac{r_0r_c}{r_0+r_c}\right) & -\frac{1}{x_l}\frac{r_0}{r_0+r_c} \\ \frac{1}{x_c}\frac{r_0}{r_0+r_c} & -\frac{1}{x_c}\frac{1}{r_0+r_c} \end{bmatrix}, b_1 = b_2 = \begin{bmatrix} \frac{v_s}{x_l}\\0\end{bmatrix}.\]
The goal is to design a controller to keep the state of the system in a safety region around the reference desired value, using as input only the switching signal. In order to study the concrete system and its symbolic abstraction in a unified framework, we will solve the problem for the sampled system with a sampling time $\tau$. For the construction of the relations in the abstraction, it is necessary to over-approximate attainable sets of a particular cell. In this example, we consider the use of a growth bound function [4, VIII.2, VIII.5] which is one of the possible methods to over-approximate attainable sets of a particular cell based on the state reach by its center.
First, let us import StaticArrays and Plots.
using StaticArrays, PlotsAt this point, we import the useful Dionysos sub-modules.
using Dionysos
const DI = Dionysos
const UT = DI.Utils
const DO = DI.Domain
const ST = DI.System
const SY = DI.Symbolic
const OP = DI.Optim
const AB = OP.AbstractionDionysos.Optim.AbstractionDefinition of the system
we can import the module containing the DCDC problem like this
include(joinpath(dirname(dirname(pathof(Dionysos))), "problems", "dc_dc.jl"));and we can instantiate the DC system with the provided system
concrete_problem = DCDC.problem()
concrete_system = concrete_problem.system
x0 = SVector(0.0, 0.0)
hx = SVector(2.0 / 4.0e3, 2.0 / 4.0e3)
state_grid = DO.GridFree(x0, hx)
u0 = SVector(1)
hu = SVector(1)
input_grid = DO.GridFree(u0, hu)
using JuMP
optimizer = MOI.instantiate(AB.UniformGridAbstraction.Optimizer)
MOI.set(optimizer, MOI.RawOptimizerAttribute("concrete_problem"), concrete_problem)
MOI.set(optimizer, MOI.RawOptimizerAttribute("state_grid"), state_grid)
MOI.set(optimizer, MOI.RawOptimizerAttribute("input_grid"), input_grid)
MOI.set(optimizer, MOI.RawOptimizerAttribute("jacobian_bound"), DCDC.jacobian_bound())
MOI.set(optimizer, MOI.RawOptimizerAttribute("time_step"), 0.5)
MOI.set(
optimizer,
MOI.RawOptimizerAttribute("approx_mode"),
AB.UniformGridAbstraction.GROWTH,
)
MOI.set(optimizer, MOI.RawOptimizerAttribute("efficient"), true)
MOI.optimize!(optimizer)
abstract_controller = MOI.get(optimizer, MOI.RawOptimizerAttribute("abstract_controller"))
concrete_controller = MOI.get(optimizer, MOI.RawOptimizerAttribute("concrete_controller"))
abstraction_time =
MOI.get(optimizer, MOI.RawOptimizerAttribute("abstraction_construction_time_sec"))
println("Time to construct the abstraction: $(abstraction_time)")
abstract_problem_time =
MOI.get(optimizer, MOI.RawOptimizerAttribute("abstract_problem_time_sec"))
println("Time to solve the abstract problem: $(abstract_problem_time)")
total_time = MOI.get(optimizer, MOI.RawOptimizerAttribute("solve_time_sec"))
println("Total time: $(total_time)")
invariant_set = MOI.get(optimizer, MOI.RawOptimizerAttribute("invariant_set"))
invariant_set_complement =
MOI.get(optimizer, MOI.RawOptimizerAttribute("invariant_set_complement"));┌ Warning: Noise is not yet accounted for in system abstraction.
└ @ Dionysos.Optim.Abstraction.UniformGridAbstraction ~/.julia/packages/Dionysos/BQJ01/src/optim/abstraction/UniformGridAbstraction/empty_problem.jl:393
compute_abstract_system_from_concrete_system!: started with Dionysos.System.DiscreteTimeGrowthBound
compute_abstract_system_from_concrete_system! terminated with success: 3776873 transitions created
compute_controller_safe! started
Safety: terminated with true
Time to construct the abstraction: 1.2201950550079346
Time to solve the abstract problem: 0.8822019100189209
Total time: 2.102452039718628Trajectory display
We choose the number of steps nsteps for the sampled system, i.e. the total elapsed time: nstep*tstep as well as the true initial state x0 which is contained in the initial state-space defined previously.
nstep = 300
x0 = SVector(1.2, 5.6)
control_trajectory = ST.get_closed_loop_trajectory(
MOI.get(optimizer, MOI.RawOptimizerAttribute("discrete_time_system")),
concrete_controller,
x0,
nstep,
);
fig = plot(; aspect_ratio = :equal);
plot!(concrete_system.X; label = "", color = :grey);
plot!(concrete_problem.initial_set; color = :green, label = "");
plot!(control_trajectory; arrows = false, ms = 2.0, color = :blue)Example: DC-DC converter solved by Uniform grid abstraction by exploiting the incremental stability of the system.
Definition of the system
we can import the module containing the DCDC problem like this
include(joinpath(dirname(dirname(pathof(Dionysos))), "problems", "dc_dc.jl"));WARNING: replacing module DCDC.and we can instantiate the DC system with the provided system
concrete_problem = DCDC.problem()
concrete_system = concrete_problem.system
origin = SVector(0.0, 0.0)
η = (2 / 4.0) * 10^(-3);Note: In the following, P and ϵ are computed by hand, but their computation is not crucial since they only affect the visualization of the abstraction. See https://github.com/dionysos-dev/Dionysos.jl/issues/345
ϵ = 0.1 * 0.01
P = SMatrix{2, 2}(1.0224, 0.0084, 0.0084, 1.0031)
state_grid = DO.GridEllipsoidalRectangular(origin, SVector(η, η), P / ϵ)
u0 = SVector(1)
hu = SVector(1)
input_grid = DO.GridFree(u0, hu)
optimizer = MOI.instantiate(AB.UniformGridAbstraction.Optimizer)
MOI.set(optimizer, MOI.RawOptimizerAttribute("concrete_problem"), concrete_problem)
MOI.set(optimizer, MOI.RawOptimizerAttribute("state_grid"), state_grid)
MOI.set(optimizer, MOI.RawOptimizerAttribute("input_grid"), input_grid)
MOI.set(optimizer, MOI.RawOptimizerAttribute("jacobian_bound"), DCDC.jacobian_bound())
MOI.set(
optimizer,
MOI.RawOptimizerAttribute("approx_mode"),
AB.UniformGridAbstraction.CENTER_SIMULATION,
)
MOI.set(optimizer, MOI.RawOptimizerAttribute("time_step"), 0.5)
MOI.optimize!(optimizer);
abstract_controller = MOI.get(optimizer, MOI.RawOptimizerAttribute("abstract_controller"))
concrete_controller = MOI.get(optimizer, MOI.RawOptimizerAttribute("concrete_controller"))
abstraction_time =
MOI.get(optimizer, MOI.RawOptimizerAttribute("abstraction_construction_time_sec"))
println("Time to construct the abstraction: $(abstraction_time)")
abstract_problem_time =
MOI.get(optimizer, MOI.RawOptimizerAttribute("abstract_problem_time_sec"))
println("Time to solve the abstract problem: $(abstract_problem_time)")
total_time = MOI.get(optimizer, MOI.RawOptimizerAttribute("solve_time_sec"))
println("Total time: $(total_time)")┌ Warning: Noise is not yet accounted for in system abstraction.
└ @ Dionysos.Optim.Abstraction.UniformGridAbstraction ~/.julia/packages/Dionysos/BQJ01/src/optim/abstraction/UniformGridAbstraction/empty_problem.jl:393
compute_abstract_system_from_concrete_system!: started with Dionysos.System.DiscreteTimeCenteredSimulation
compute_abstract_system_from_concrete_system! terminated with success: 932213 transitions created
compute_controller_safe! started
Safety: terminated with true
Time to construct the abstraction: 0.5933210849761963
Time to solve the abstract problem: 0.5435700416564941
Total time: 1.136944055557251Trajectory display
We choose the number of steps nsteps for the sampled system, i.e. the total elapsed time: nstep*tstep as well as the true initial state x0 which is contained in the initial state-space defined previously.
nstep = 300
x0 = SVector(1.2, 5.6)
control_trajectory = ST.get_closed_loop_trajectory(
MOI.get(optimizer, MOI.RawOptimizerAttribute("discrete_time_system")),
concrete_controller,
x0,
nstep,
)
fig = plot(; aspect_ratio = :equal);
plot!(concrete_system.X; label = "", color = :grey);
plot!(invariant_set_complement; color = :black, label = "Invariant set complement")
plot!(concrete_problem.initial_set; color = :green, label = "");
plot!(control_trajectory; arrows = false, ms = 2.0, color = :blue)References
- A. Girard, G. Pola and P. Tabuada, "Approximately Bisimilar Symbolic Models for Incrementally Stable Switched Systems," in IEEE Transactions on Automatic Control, vol. 55, no. 1, pp. 116-126, Jan. 2010.
- S. Mouelhi, A. Girard, and G. Gössler. “CoSyMA: a tool for controller synthesis using multi-scale abstractions”. In: HSCC. ACM. 2013, pp. 83–88.
- A. Girard. “Controller synthesis for safety and reachability via approximate bisimulation”. In: Automatica 48.5 (2012), pp. 947–953.
- G. Reissig, A. Weber and M. Rungger, "Feedback Refinement Relations for the Synthesis of Symbolic Controllers," in IEEE Transactions on Automatic Control, vol. 62, no. 4, pp. 1781-1796.
This page was generated using Literate.jl.
