Abstraction-based control

Given a mathematical description of the system dynamics and the specifications describing the desired closed-loop behavior of the system, abstraction-based control techniques involve synthesizing a correct-by-construction controller through a systematic three-step procedure. First, both the original system and the specifications are transposed into an abstract domain, resulting in an abstract system and corresponding abstract specifications. We refer to the original system as the concrete system as opposed to the abstract system. Next, an abstract controller is synthesized to solve this abstract control problem. Finally, in the third step, called concretization as opposed to abstraction, a controller for the original control problem is derived from the abstract controller.

In practice, the abstract domain is constructed by discretizing the concrete state space of the concrete system into subsets (called cells). The value of this approach lies in the substitution of the concrete system (often a system with an infinite number of states) with a finite state system, which makes it possible to leverage powerful control tools from the graph-theoretic field, such as Dijkstra or the A-star algorithm. This three steps procedure is illustrated on the following figure.

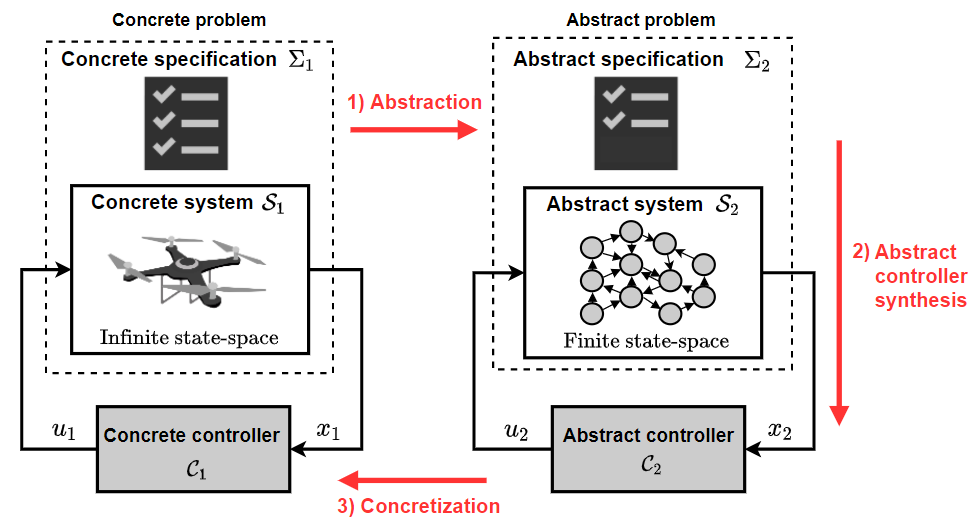
Although this approach offers a safety-critical framework, it suffers from the curse of dimensionality due to the exponential growth of the number of states with respect to the dimension. In order to render these techniques practical, it is necessary to construct smart abstractions, i.e., they differ from classical techniques in that the partitioning is designed smartly, using optimization-based design techniques, and computed iteratively, unlike the classical approach which uses an a priori defined approach, sub-optimal and subject to the curse of dimensionality. To this end, we propose solvers called lazy solvers (i.e. postponing heavier numerical operations) that co-design the abstraction and the controller to reduce the computed part of the abstraction.